1. Introduction to Programming Concepts

"There is no royal road to geometry."
"Just follow the yellow brick road."
- Euclid's reply to Ptolemy, Euclid (c. 300 BC)
- The Wonderful Wizard of Oz, L. Frank Baum (1856–1919)

• In this chapter, you will get introduced to the most important concepts in programming.
  • Later chapters will give a deeper understanding of these concepts (and add other concepts).

1. Calculator

• In Mozart, type: {Browse 9999*9999}
  • To compile that line, press: ctrl-. ctrl-l
• Result: 99980001
• Info:
  • The curly braces are used for a procedure or function call.
  • Browse is a procedure that displays the one argument in the browser window.

2. Variables

• Declare a variable (press ctrl-. ctrl-b to compile the whole buffer):

declare
V = 9999 * 9999
{Browse V*V}

• Info:
  • Variables are short-cuts for values, they cannot be assigned more than once. You can declare another variable with the same name.
  • The declare statement creates a new store variable and makes the variable identifier refer to it.
• Result: 9996000599960001

Exercise 1

• Calculate 2^8 without eight multiplications (using only variables and multiplications).
  Hint

  Use variables to store intermediate results.

Exercise 2

• Calculate 100! without typing 1*2*3... until 100. Can it be done?
  Hint

  It can't be done (that simply).

3. Functions

Factorial

• Factorial definition:
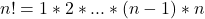
• Factorial of 10: {Browse 1*2*3*4*5*6*7*8*9*10}
• Result: 3628800
• Define a function:

declare
fun {Fact N}
    if N==0 then
        1
    else
        N*{Fact N-1}
    end
end

• Info:
  • The function body contains the if expression instruction.
  • Recursion: function is calling itself.
  • Fact mathematical recursive definition:
    • 
    • 
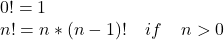
• Call the function {Fact 10} inside of the Browse procedure to display the result: {Browse {Fact 10}}
• Result: 3628800
• {Browse {Fact 100}}
• Result: 933 26215 44394 41526 81699 23885 62667 00490 71596 82643 81621 46859 29638 95217 59999 32299 15608 94146 39761 56518 28625 36979 20827 22375 82511 85210 91686 40000 00000 00000 00000 00000

Combinations

• Combination definition:
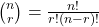
• Combination defined in Oz:

declare
fun {Comb N R}
    {Fact N} div ({Fact R}*{Fact N-R})
end

• Info:
  • Functional abstraction: using existing functions to define a new function.
• {Comb 10 3}
• Result: 120

4. Lists

• List is a sequence of elements: {Browse [5 6 7 8]}
• [5 6 7 8] is a short-cut.
  • A list is a chain of links, and each link contains two things: a list element and a reference to the rest of the chain.
  • [6 7] is linked as follows: 6 -> 7 -> nil, where nil is the empty list.
    • In Oz: Z=nil Y=7|Z X=6|Y
    • Now X references the list [6 7].
• H|T is a list pair (often called a cons)
• Example:

declare
H = 5
T = [6 7 8]
{Browse H|T}

• Result: [5 6 7 8]
• Info:
  • H|T = 5 | [6 7 8]
  • Head: 5
  • Tail: [6 7 8]
• Get back the head and tail:

declare
L = [5 6 7 8]
{Browse L.1}
{Browse L.2}

• Result:

5
[6 7 8]

Pattern matching

declare
L = [5 6 7 8]
case L of H|T then
    {Browse H} {Browse T}
end

• Result is the same as the last: 5 and [6 7 8].
• Info:
  • Case instruction declares two local variables: H and T.
  • Case decomposes L according to the pattern H|T.

5. Functions over lists

• Pascal's triangle:

   1
  1 1
 1 2 1
1 3 3 1

• We will define a function, {Pascal N}, which calculates the nth row of Pascal's triangle.
• Calculating the fifth row from the fourth:
  • Fourth row: [1 3 3 1]
  • Shift the fourth row left and right (by adding a zero to the right and left), and sum them.
    • [1 3 3 1 0] + [0 1 3 3 1] = [1 4 6 4 1], which is the fifth row.

Pascal's triangle in Oz:

declare Pascal AddList ShiftLeft ShiftRight

fun {Pascal N}
    if N==1 then [1]
    else
        {AddList {ShiftLeft {Pascal N-1}}
                 {ShiftRight {Pascal N-1}}}
    end
end

fun {ShiftLeft L}
    case L of H|T then
        H|{ShiftLeft T}
    else [0] end
end

fun {ShiftRight L} 0|L end

fun {AddList L1 L2}
    case L1 of H1|T1 then
        case L2 of H2|T2 then
            H1+H2|{AddList T1 T2}
        end
    else nil
    end
end

• Info:
  • Top-down software development: first writing the main function and filling in the blanks afterwards.
• Execute: {Pascal 20}
• Result: [1 19 171 969 3876 11628 27132 50388 75582 92378 92378 75582 50388 27132 11628 3876 969 171 19 1]

6. Complexity

• The Pascal function defined above gets very slow with larger numbers.

fun {Pascal N}
    if N==1 then [1]
    else
        {AddList {ShiftLeft {Pascal N-1}}
                 {ShiftRight {Pascal N-1}}}
    end
end

• Why?
  Answer

  Calling {Pascal N} will call {Pascal N-1} two times.
  Calling {Pascal 30} will call {Pascal 1} 2^29 times, which is about half a billion.
• FastPascal function definition:

fun {FastPascal N}
    if N==1 then [1]
    else L in
        L = {FastPascal N-1}
        {AddList {ShiftLeft L} {ShiftRight L}}
    end
end

• Info:
  • Local variable is declared with L in: that is just like using declare, except the variable exists only between the else and the end.
• Time complexity:
  • The execution time of a program as a function of input size.
  • Time complexity of {Pascal N} and {FastPascal N}?
  Answer

  {Pascal N}: ~2^n
  {FastPascal N}: ~n^2

7. Lazy evaluation

• Up until now everything we did was with eager evaluation, functions did their calculations as soon as they were called.
• Lazy evaluation: a calculation is done only when the result is needed.
• Example function that calculates a list of integers, from N to infinity:

fun lazy {Ints N}
    N | {Ints N+1}
end

• Info:
  • {Ints 0} calculates the infinite list 0|1|2|3|4|... which looks like an infinite loop.
  • Lazy evaluation ensures that the function will calculate only what is needed.
  • {Ints 0} will display nothing, as nothing yet needed to be calculated.
  • {Ints 0}.1 will display 0 as that is the head (the first element) of the list.
• case {Ints 0} of A|B|C|_ then {Browse A+B+C} end displays 3.

Exercise 3

• Define a function that calculates the sum of a list of integers:

fun {SumList L}
    case L of X|L1 then X+{SumList L1}
    else 0 end
end

• What happens if we call {SumList {Ints 0}}? Is this a good idea?
  Hint

  Sum needs each of the elements in the list.

Lazy calculation of Pascal's triangle

fun lazy {PascalList Row}
    Row | { PascalList
                {AddList {ShiftLeft Row}
                         {ShiftRight Row}} }
end

declare
L = {PascalList [1]}

• Try:
  • {Browse L}
  • {Browse L.1}
  • {Browse L.2.1}

Exercise 4

• Instead of writing a lazy function, we can write a function that directly calculates N rows starting from an initial Row:

fun {PascalList2 N Row}
    if N==1 then
        [Row]
    else
        Row | {PascalList2 N-1
                   {AddList {ShiftLeft Row}
                            {ShiftRight Row}}}
    end
end

• Why is the lazy version better? Think of an example in which the lazy version is the more optimal solution.
  Hint1

  {Browse {PascalList2 10 [1]}} would display the first 10 rows of the Pascal's triangle.
  What if we call the function again, but this time we want the first 11 rows? How is the lazy version more optimal?

  Hint2

  Lazy evaluation does not calculate twice, it can continue where it left off.

8. Higher-order programming

• We define a generic function that accepts a function as an argument, so we can construct different variations of Pascal's triangle with operations other than addition:

fun {GenericPascal Op N}
    if N==1 then [1]
    else L in
        L = {GenericPascal Op N-1}
        {OpList Op {ShiftLeft L} {ShiftRight L}}
    end
end

fun {OpList Op L1 L2}
    case L1 of H1|T1 then
        case L2 of H2|T2 then
            {Op H1 H2}|{OpList Op T1 T2}
        end
    else nil end
end

• Info:
  • The ability to pass functions as arguments is known as higher-order programming.
  • We are using the old versions of ShiftLeft and ShiftRight, AddList is replaced with OpList.

Exercise 5

• Define the function Add such that when used in {GenericPascal Add N} you get the same result as with the original Pascal function.
  Hint

  Function Add should perform addition of the two numbers passed as arguments.
• Define the function Xor that does an exclusive-or operation, and try using it in {GenericPascal Xor N}.
  Hint

  X	Y	X xor Y
  0	0	0
  0	1	1
  1	0	1
  1	1	0

• Additional info:
  • The Xor Pascal's triangle shows for each number in the Pascal's triangle if it is odd or even (without calculating the numbers).
  • When visualized, it resembles Sierpiński triangle:

Assignment 1

• Use this loop instruction to explore the Pascal's triangle variations: for I in 1..10 do {Browse {GenericPascal Op I}} end
• Try variations with operations: subtraction, multiplication, etc.
  • Why does multiplication give a triangle with all zeroes?
  • Make a new multiplication function that will avoid the problem above.

9. Concurrency

• Concurrency allows several independant activities to execute at their own pace.
• Difference between concurrency and parallelism:

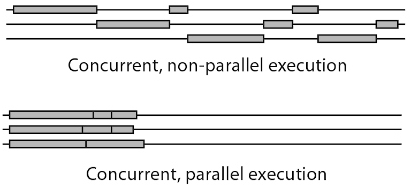
• Calling the slow Pascal function in its thread, concurrently:

thread P in
    P = {Pascal 25}
    {Browse P}
end
{Browse 99*99}

• Info:
  • This creates a new thread.
  • Inside of the thread, {Pascal 25} is calculated and displayed.
  • The thread takes some time to finish, but the result of 99*99 is displayed immediately wihout waiting for Pascal to finish.

10. Dataflow

• Dataflow: if a variable is not yet bound to a value the operation that needs that variable will wait until the variable is bound (in another operation or thread).
• Simple dataflow example:

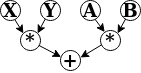
• Dataflow and concurreny:

declare X
thread
   {Delay 5000}
   X=99
end
{Browse start} {Browse X*X}

• Dataflow properties:
  • Calculations work correctly independant of how they are partitioned between threads.
  • Calculations are patient, they do not signal errors (they just wait).

11. State

• Functions that can change their behaviour and learn from their past need memory to do so.
• That kind of memory is called explicit state.

A memory cell

• A memory cell is one way to define explicit state.
• Normally you call a memory cell "variable", not to confuse it with the variables in the previous sections which are more like mathematical variables (shortcuts for values, not storages).
• Example usage:

declare
C = {NewCell 0}
C := @C + 1
{Browse @C}

• Info:
  • C = {NewCell 0} creates a cell C with initial content 0.
  • In C := @C + 1:
    • @C reads the current value,
    • + 1 adds one to that value,
    • C := writes the new value into the cell.
  • {Browse @C} displays the value stored in C.

Assignment 2

• You are given two code fragments, the first uses variables:

local X in
    X = 23
    local X in
        X = 44
    end
    {Browse X}
end

• The second uses a cell:

local X in
    X = {NewCell 23}
    X := 44
    {Browse @X}
end

• In the first, the indentifier X refers to two different variables. In the second, X refers to a cell.
  • What does Browse display in each fragment? Explain.

Adding memory to a function

• A simple function with memory that counts how many times the function was called:

declare
C = {NewCell 0}
fun {Add A B}
   C := @C + 1
   A + B
end

Exercise 6

• Define two functons, Bump and Read:
  • Bump adds one to the counter (to a memory cell) and returns the current value of that cell,
  • Read returns the current value of the memory cell.

Assignment 3

• Let us define a function {Accumulate N} that accumulates all its inputs.
• Example:

{Browse {Accumulate 5}}
{Browse {Accumulate 100}}
{Browse {Accumulate 45}}

• This should display 5, 105, and 150.
• Here is a wrong way to write Accumulate:

declare
fun {Accumulate N}
    Acc in
        Acc = {NewCell 0}
        Acc := @Acc + N
        @Acc
end

• What is wrong with this definition?
  • Correct it.

12. Objects

• In the previous exercise you implemented functions Bump and Read that update and read a memory cell.
  • You actually implemented an object, which can be improved (in the next exercise).
• The Bump/Read object writes and reads from a memory cell. That memory cell can be accessed from anywhere in the program (which is not secure).
• To make that object better, we can isolate the memory cell so it can be accessed only from the inside of the object.
  • This property is called encapsulation.

Exercise 7

• Improve the Bump/Read object implementation by referencing the memory cell C with a local variable:

declare
local C in
    %% your implementation of the object %%
end

13. Classes

• In the last section we defined one counter object (Bump/Read).
• It would be useful to have more than one counter object, so we can count different things at different rates.
• Class is a factory that produces objects.
• Below is a class that creates instances of the counter:

declare
fun {NewCounter}
    C Bump Read in
        C = {NewCell 0}
        fun {Bump}
            C := @C + 1
            @C
        end
        fun {Read}
            @C
        end
        counter(bump:Bump read:Read)
end

• Info:
  • NewCounter is a function that creates a new (local) cell and returns new Bump and Read functions for it.
    • A function returning a function is another form of higher-order programming.
  • Functions Bump and Read are grouped together into one data structure called a record - counter(bump:Bump read:Read).
    • The record has a label ("counter"), and two fields ("bump" and "read").
• Now we can create two counters and use them:

declare
Ctr1 = {NewCounter}
Ctr2 = {NewCounter}

{Browse {Ctr1.bump}}
{Browse {Ctr1.bump}}
{Browse {Ctr2.read}}

• Info:
  • Each counter has its own internal memory.
  • We access functions Bump and Read with the "." (dot) operator.
• Programming with classes and objects is called object-based programming.
  • Adding inheritance to object-based programming gives object-oriented programming.
  • Inheritance: a new class can be defined in terms of existing classes by specifying how the new class is different.

14. Nondeterminism and time

• Nondeterminism by itself is not a problem, we already have it with concurrency.
  • We lack the knowledge of the exact time when each operation executes (in different threads).
  • Nondeterminism becomes difficult when it becomes observable (race condition).
• Having both explicit state and concurrency at the same time becomes tricky (nondeterminism becomes observable).
  • The same program can give different results from one execution to the next because the order in which threads access the state can change from one execution to the next.
• An example of observable nondeterminism (race condition):

declare
C = {NewCell 0}
thread
    C := 1
end
thread
    C := 2
end

• What is the content of C after this program executes?
• Second example of observable nondeterminism:

declare
C = {NewCell 0}
thread I in
    I = @C
    C := I + 1
end
thread J in
    J = @C
    C := J + 1
end

• What is the content of C after this program executes?
  Hint1

  Thread execution is interleaved.

  Hint2

  
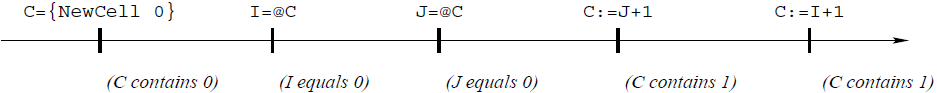
• Programming with explicit state and concurrency:
  • If possible, do not use state and concurrency together (as their interaction brings complications).
  • If a program does need to have both, it is probably possible to design it so state and concurrency interact only in a very small part of the program.

15. Atomicity

• An operation is atomic if no intermidiate states can be observed.
• A solution to the interleaving problem from the previous example is to make each thread body (that interacts with the same memory cell) atomic.
  • With a new language entity, lock.
  • A lock has the property that only one thread at a time can be executing inside.

declare
C = {NewCell 0}
L = {NewLock}
thread
    lock L then I in
        I = @C
        C := I + 1
    end
end
thread
    lock L then J in
        J = @C
        C := J + 1
    end
end

• Info:
  • In this version the final result is always 2.
  • {NewLock} creates a new lock.
  • lock L then ... end: code between then and end is inside of the lock L.

---

< ^ >