2. Declarative Programming Techniques

"The nice thing about declarative programming is that you can write a specification and run it as a program. The nasty thing about declarative programming is that some clear specifications make incredibly bad programs. The hope of declarative programming is that you can move from a specification to a reasonable program without leaving the language."
- The Craft of Prolog, Richard O’Keefe

• An operation is declarative if it always returns the same results (when called with the same arguments) independent of any other computation state.
• A declarative operation is:
  • independent,
  • stateless,
  • deterministic.
• Declarative programming is important because of two properties:
  • Declarative programs are compositional.
    • They consist of components that can each be written, tested, and proved correct independently of other components and of their own past history (previous calls).
  • Reasoning about declarative programs is simple.
    • Simple algebraic and logical reasoning can be used.
• Not all programs can be easily written in the declarative model.
  • As many components (in a program) as possible should be declarative.
• This chapter explains how to write practical declarative programs.
• The basic technique for writing declarative programs:
  • Consider the program as a set of recursive function definitions.
  • Use high-orderness to simplify the program structure.

1. Iterative computation

• An iterative computation is a loop whose stack size is bounded by a constant (independent of the number of iterations).

General schema

• Starts with an initial state S₀ and transforms the state in steps until reaching a final state S_final:
  • S₀ -> S₁ -> ... -> S_final
• General schema:

• Info:
  • Functions IsDone and Transform are problem dependent.
  • Stack size does not grow when executing Iterate.

Newton's method

• Newton's method for calculating the square root of a positive real number x is an iterative computation.
• It starts with a guess g and improves that guess iteratively until it is accurate enough.
• The improved guess g' is the average of g and x/g.
  • g' = (g + x/g) / 2

fun {Sqrt X}
    Guess = 1.0
in
    {SqrtIter Guess X}
end

fun {SqrtIter Guess X}
    if {GoodEnough Guess X} then Guess
    else
        {SqrtIter {Improve Guess X} X}
    end
end

fun {Improve Guess X}
    (Guess + X/Guess) / 2.0
end

fun {GoodEnough Guess X}
    {Abs X-Guess*Guess}/X < 0.00001
end

fun {Abs X} if X<0.0 then ~X else X end end

• Additional info:
  • Video about Newton's method, polynomials, and fractals

Assignment 1

• Define a function Abs that calculates the absolute value of a real number.
• The following definition does not work:

declare
fun {Abs X}
    if X<0 then ~X
    else X
    end
end

• Why not? Correct it.
  Hint

  The problem is trivial.

Assignment 2

• Define a Cbrt function (cube root) that uses the Newton's method to calculate it.
  • The formula for calculating the improved guess: g' = (2g + x/g²) / 3

Using local procedures

• Several helper functions are defined in the Newton's method program above: SqrtIter, Improve, GoodEnough, and Abs.
• Where to define helper functions?
  • A function defined only as an aid to define another function should not be visible elsewhere.
• Dependency:
  • SqrtIter is needed in Sqrt,
  • Improve and GoodEnough are needed in SqrtIter,
  • Abs is a utility function that could be used elsewhere.
• There are two basic ways to express this visibility:
  1. All the helper functions are defined in a local statement outside of Sqrt.
  2. Each helper function is defined inside of the function that needs it.

Way 1

• All the helper functions are defined in a local statement outside of Sqrt.

local
    fun {Improve Guess X} ... end
    fun {GoodEnough Guess X} ... end
    fun {SqrtIter Guess X}
        if {GoodEnough Guess X} then Guess
        else
           {SqrtIter {Improve Guess X} X}
        end
    end
end
in
    fun {Sqrt X}
        Guess=1.0
    in
        {SqrtIter Guess X}
    end
end

Way 2

• Each helper function is defined inside of the function that needs it.

fun {Sqrt X}
    fun {SqrtIter Guess X}
        fun {Improve Guess X} ... end
        fun {GoodEnough Guess X} ... end
    in
        if {GoodEnough Guess X} then Guess
        else
            {SqrtIter {Improve Guess X} X}
        end
    end
    Guess=1.0
in
    {SqrtIter Guess X}
end

Way 2, simplified

• Each helper function sees the arguments of its enclosing function as external references.
  • This means we can remove these arguments from the helper functions.

fun {Sqrt X}
    fun {SqrtIter Guess}
        fun {Improve} ... end
        fun {GoodEnough} ... end
    in
        if {GoodEnough} then Guess
        else
            {SqrtIter {Improve}}
        end
    end
    Guess=1.0
in
    {SqrtIter Guess}
end

Final definition

• There is a trade-off between putting the helper definitions outside the function that needs them or putting them inside:
  • Putting them inside lets them see the arguments of the main function (therefore they need fewer arguments). But each time the main function is called, new helper functions are created.
  • Putting them outside means that the functions are created once, for all calls to the main function. But then the helper functions need more arguments.
• The final definition (below) balances that trade-off (between efficiency and visibility).
  • SqrtIter is local to Sqrt.
  • Improve and GoodEnough are outside SqrtIter.

fun {Sqrt X}
    fun {Improve Guess} ... end
    fun {GoodEnough Guess} ... end
    fun {SqrtIter Guess}
        if {GoodEnough Guess} then Guess
        else
            {SqrtIter {Improve Guess}}
        end
    end
    Guess=1.0
in
    {SqrtIter Guess}
end

Control abstraction

• Here is once again the schema for the iteration control flow:

• We will now turn that schema into a program component, making the schema a control abstraction.
  • The schema has to be parameterized by extracting the parts that vary from one use to another.
    • IsDone and Transform are such parts.

fun {Iterate S IsDone Transform}
    if {IsDone S} then S
    else S1 in
        S1 = {Transform S}
        {Iterate S1 IsDone Transform}
    end
end

• Info:
  • Arguments IsDone and Transform accept one-argument functions.
• We can make Iterate behave like SqrtIter by passing it the functions GoodEnough and Improve:

fun {Sqrt X}
    { Iterate
        1.0
        fun {$ G} {Abs X-G*G}/X < 0.00001 end
        fun {$ G} (G+X/G)/2.0 end }
end

• This is a powerful way to structure a program because it separates the general control flow from this particular use.

Assignment 3

• The half-interval method is a technique for finding roots of a function f (the x values such that the function f(x) = 0), where f is a continuous real function.
• If we are given points a and b such that f(a) < 0 < f(b), then f must have at least one root between a and b.
• Steps to calculate a root:
  • Let x = (a+b)/2 and compute f(x).
  • If f(x) > 0 then f must have a root between a and x, otherwise the root is between x and b.
  • Repeat until the calculated x is accurate enough.
• Write a declarative program to solve this problem using the techniques of iterative computation.
  • {HalfInterRoot F A B}
    • Pass a continuous real function to the argument F.
    • Pass values a and b to arguments A and B.
    • Return a value that approximates a root of the function.
    Example

    Roots of the function: f(x) = x²-2
    

2. Recursive computation

• Iterative computation is a special case of recursive computation.
  • While iterative computation calls itself once (and has a constant stack size), recursive computation can call itself more than once.
• Recursion occurs in two major ways: in functions and in data types.
  • A function is recursive if its definition has at least one call to itself.
  • A data type is recursive if it is defined in terms of itself (e.g., list).

Print Gallery (M. C. Escher)

• Iterative computation has a constant stack size, which is not always the case with recursive computation.
  • It is important to avoid growing stack size whenever possible.
• The factorial implementation below is an example of a recursive computation that is not iterative (its stack size is growing).
• Factorial mathematical definition:

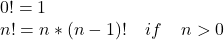
• Implementation:

fun {Fact N}
    if N==0 then 1
    elseif N>0 then N*{Fact N-1}
    else raise domainError end
    end
end

• Info:
  • This defines the factorial of a big number in terms of the factorial of a smaller number.
  • Since all numbers are nonnegative, they will bottom out at zero.

Growing stack size

• In the factorial implementation above, multiplication comes after the recursive call (tail recursion).
  • During the recursive call the stack has to keep information about the multiplication for when the recursive call returns.

Converting a recursive to an iterative computation

• Previous implementation for factorial calculation:
  • 3! = (3*(2*(1*1)))
• We can rearrange the numbers like this:
  • 3! = (((1*3)*2)*1)
• The second calculation can be done incrementally.
• The iterative definition that calculates factorial in this way is:

fun {Fact N}
    fun {FactIter N A}
        if N==0 then A
        elseif N>0 then {FactIter N-1 A*N}
        else raise domainError end
        end
    end
in
    {FactIter N 1}
end

• Info:
  • The function that does the iteration, FactIter, has a second argument A without which iterative factorial would not be possible. It effectively serves as memory for the intermediate results of multiplication.

3. Programming with recursion

• This section shows basic techniques for programming with lists, queues, and trees.

Programming with lists

• The basic techniques of programming with lists are:
  • Thinking recursively (solve a problem in terms of smaller versions of the problem).
  • Converting recursive to iterative computations (naive list programs are often wasteful).
  • Constructing programs by following the type (recursive structure of a program often closely mirrors the definition of a type with which it calculates).

Thinking recursively

• A list is a recursive data structure: it is defined in terms of a smaller version of itself.
• The function that calculates on lists consists of two parts:
  • A base case: For small lists, the function computes the answer directly.
  • A recursive case: For bigger lists, the function computes the result in terms of the results of one or more smaller lists.
• Example of a recursive function that calculates the length of a list:

fun {Length Ls}
    case Ls
    of nil then 0
    [] _|Lr then 1+{Length Lr}
    end
end
{Browse {Length [a b c]}}

• Info:
  • The base case is the empty list nil, for which the function returns 0.
  • The recursive case is any other list.
  • If the list has length n, then its tail has length n-1. As the tail is smaller than the original list, the program will terminate.
• Example of a function that appends two lists Ls and Ms together to make a third list:

fun {Append Ls Ms}
    case Ls
    of nil then Ms
    [] X|Lr then X|{Append Lr Ms}
    end
end

• Info:
  • The function follows two properties of append:
    • append(nil, m) = m
    • append(x|t, m) = x | append(t, m)
  • The recursive case always calls Append with a smaller first argument, so the program terminates.

Exercise 1

• Define the function Nth to get the nth element of a list.
  • {Nth Xs N}, where Xs is a list and N an integer.
  Help

  Base case: if N is 1, return the head of the list.
  Recursive case: if N>1, calculate *Nth* on the tail.

Exercise 2

• Define the function SumList that sums all the elements of a list of integers.
  • {SumList Xs}, where Xs is a list.
  Help

  Base case: in case Xs is nil, return 0.
  Recursive case: otherwise, when Xs is of shape "X|Xr", then sum the head with the result of *SumList* on the tail.

Naive recursive definition

• Let us define a function to reverse the elements of a list.
• Recursive definition of list reversal:
  • reverse(nil) = nil.
  • reverse(X|Xs) = append( reverse(Xs), [X] ).
• Implementation:

fun {Reverse Xs}
    case Xs
    of nil then nil
    [] X|Xr then
        {Append {Reverse Xr} [X]}
    end
end

• Reverse execution time:
  • N recursive calls (which contain calls to Append).
  • Each Append call will process a list of length n/2 on average.
  • The total execution time is therefore proportional to n*n/2, namely n².
  • We would expect that reversing a list would take time proportional to the input length and not to its square.
• Reverse stack size:
  • The stack size grows with the input list length (recursive computation that is not iterative).
• Naively following the reverse recursive definition has given us an inefficient result.

Converting recursive to iterative computations

• Here we will see how to convert recursive computations into iterative ones.
• Instead of using Reverse, we first use a simpler function that calculates the length of a list.
• Naive implementation:

fun {Length Xs}
    case Xs of
    nil then 0
    [] _|Xr then
        1+{Length Xr}
    end
end

• This function is linear in time, but the stack size is proportional to the recursive depth.
  • This occurs because the addition 1+{Length Xr} happens after the recursive call.
• Iterative implementation:

local
    fun {IterLength I Ys}
        case Ys
        of nil then I
        [] _|Yr then
            {IterLength I+1 Yr}
        end
    end
in
    fun {Length Xs}
        {IterLength 0 Xs}
    end
end

• Info:
  • It uses an accumulator that effectively serves as a memory for length (the first argument in IterLength function).
• We can use the same technique on Reverse.
  • Use the accumulator as memory for "the reverse of the part of the list already seen" instead of its length.

local
    fun {IterReverse Rs Ys}
        case Ys
        of nil then Rs
        [] Y|Yr then
            {IterReverse Y|Rs Yr}
        end
    end
in
    fun {Reverse Xs}
        {IterReverse nil Xs}
    end
end

• Now, the Reverse implementation should be both linear-time and iterative computation.

Assignment 4

• Rewrite the function SumList (from Exercise 2) to be iterative using the techniques developed for Length.

Assignment 5

• The Append implementation from a previous section is iterative (the stack size is constant):

fun {Append Ls Ms}
    case Ls
    of nil then Ms
    [] X|Lr then X|{Append Lr Ms}
    end
end

• It is iterative in the declarative paradigm (which has dataflow variables, allowing the unfinished list to have unbound variables).
• In the functional paradigm (which is a subset of the declarative paradigm), where variables must be immediately bound, the implementation above is not iterative.
  • In the functional paradigm the stack size would be proportional to the recursive depth because the list appending operation ("|") would execute after the recursion.
• Write an iterative append that would be iterative even in the functional paradigm (restrict the declarative paradigm to calculate with values only - no unbound variables).
  • You will need the Reverse function and a new iterative function that appends the reverse of a list to another list (which is not reversed).
  Hint

  [1 2] + [3 4] -> append( reverse([1 2]), [3 4] )
  [2 1], [3 4] -> 2 | [3 4]
  [1], [2 3 4] -> 1 | [2 3 4]
  [], [1 2 3 4]

Sorting with mergesort

• Let's define a function that takes a list of numbers and returns a new list sorted in ascending order.
• We use the mergesort algorithm which is based on a simple divide-and-conquer strategy:
  • Split the list into two smaller lists (of approximately equal length).
  • Use mergesort recursively to sort two smaller lists.
  • Merge the two sorted lists together.

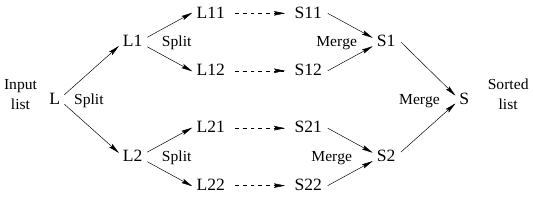
proc {Split Xs ?Ys ?Zs}
    case Xs
    of nil then Ys=nil Zs=nil
    [] [X] then Ys=[X] Zs=nil
    [] X1|X2|Xr then Yr Zr in
        Ys=X1|Yr
        Zs=X2|Zr
        {Split Xr Yr Zr}
    end
end

fun {Merge Xs Ys}
    case Xs # Ys
    of nil # Ys then Ys
    [] Xs # nil then Xs
    [] (X|Xr) # (Y|Yr) then
        if X<Y then X|{Merge Xr Ys}
        else Y|{Merge Xs Yr}
        end
    end
end

fun {MergeSort Xs}
    case Xs
    of nil then nil
    [] [X] then [X]
    else Ys Zs in
        {Split Xs Ys Zs}
        {Merge {MergeSort Ys} {MergeSort Zs}}
    end
end

Accumulators

• Accumulator programming is a technique for writing iterative computations (used in IterLength and IterReverse functions we saw before).
• The main idea is to carry state forward at all times and never do a return calculation.

Mergesort with an accumulator

• The previous definition of mergesort first calls the function Split to divide the input list into two halves.
• The simpler way to do mergesort is by using an accumulator.
  • The parameter represents "the part of the list still to be sorted."
• The specification of MergeSortAcc:
  • S#L2 = {MergeSortAcc L1 N} takes an input list L1 and an integer N. It returns two results: S, the sorted list of the first N elements of L1, and L2, the remaining elements of L1. The two results are paired together with the # tupling constructor.
• Implementation:

fun {MergeSort Xs}
    fun {MergeSortAcc L1 N}
        if N==0 then
            nil # L1
        elseif N==1 then
            [L1.1] # L1.2
        elseif N>1 then
            NL = N div 2
            NR = N-NL
            Ys # L2 = {MergeSortAcc L1 NL}
            Zs # L3 = {MergeSortAcc L2 NR}
        in
            {Merge Ys Zs} # L3
        end
    end
in
    {MergeSortAcc Xs {Length Xs}}.1
end

• This version has the same time complexity as the previous version, but it uses less memory because it does not create the two split lists.

Queues

• A queue is a sequence of elements with an insert and a delete operation.
  • The insert operation adds an element to one end of the queue and the delete operation removes an element from the other end.
  • Queues have FIFO (First-In-First-Out) behavior.

A naive queue

• If a list L represents the queue content, then inserting X gives the new queue X|L. Deleting Y is done by calling {ButLast L Y L1} (which binds Y to the deleted element and returns the new queue in L1):

declare L X L1

proc {ButLast L ?X ?L1}
    case L
    of [Y] then X=Y L1=nil
    [] Y|L2 then L3 in
        L1 = Y|L3
        {ButLast L2 X L3}
    end
end

L = [1 2 3 4]
{ButLast L X L1}
{Browse L1}
{Browse X}

• ButLast is slow: it takes time proportional to the number of elements in the queue.

Amortized constant-time ephemeral queue

• Amortized constant-time: a sequence of n function/procedure calls takes a total time that is proportional to some constant times n.
• Ephemeral queue: there can be only one version of the queue in use at any time.
• Definition of an ephemeral queue that has amortized constant-time:

fun {NewQueue} q(nil nil) end

fun {Check Q}
    case Q of q(nil R) then q({Reverse R} nil) else Q end
end

fun {Insert Q X}
    case Q of q(F R) then {Check q(F X|R)} end
end

fun {Delete Q X}
    case Q of q(F R) then F1 in F=X|F1 {Check q(F1 R)} end
end

fun {IsEmpty Q}
    case Q of q(F R) then F==nil end
end

• Info:
  • This uses the pair q(F R) to represent the queue. F and R are lists.
  • F represents the front of the queue and R represents the back of the queue in reverse.
  • In "Delete" function, "F=X|F1" binds the head of list F to X and the tail to F1.
• Example:

Q1 = {NewQueue}         % Q1 = q(nil nil)
Q2 = {Insert Q1 1}      % Q2 = q([1] nil)
Q3 = {Insert Q2 2}      % Q3 = q([1] [2])
Q4 = {Insert Q3 3}      % Q4 = q([1] [3 2])
Q5 = {Insert Q4 4}      % Q5 = q([1] [4 3 2])
Q6 = {Insert Q5 5}      % Q6 = q([1] [5 4 3 2])

Q7 = {Delete Q6 X}      % Q7 = q([2 3 4 5] nil)  X=1
Q8 = {Delete Q7 X}      % Q8 = q([3 4 5] nil)    X=2

Q9  = {Insert Q8 6}     % Q9  = q([3 4 5] [6])
Q10 = {Insert Q9 7}     % Q10 = q([3 4 5] [7 6])

Q11 = {Delete Q10 X}    % Q11 = q([4 5] [7 6])   X=3

Assignment 6

• Consider the FIFO queue defined above.
  • What happens if you delete an element from an empty queue? Explain.

Trees

• Trees are recursive data structures.
• A tree is either a leaf node or a node that contains one or more trees.
• Nodes can carry additional information.
• One possible definition:

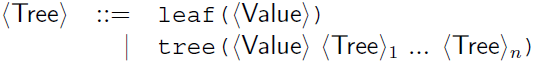
• One of many applications for the tree structure: https://www.youtube.com/watch?v=TrrbshL_0-s

Ordered binary tree

• An ordered binary tree (OBTree) is a binary tree in which each node includes a pair of values:

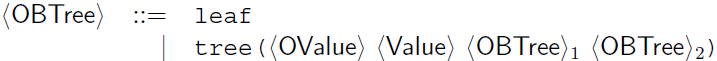
• Non-leaf nodes include the values OValue and Value.
  • OValue (Ordered Value) is a value by which the nodes in a tree are ordered - Key.
  • Value is carried along with no particular condition imposed on it - Information.

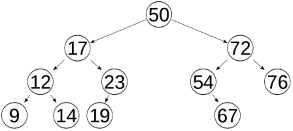
Storing information in trees

• An ordered binary tree can be used as a repository of information.
  • We have to define three operations: looking up, inserting, and deleting entries.
• Looking up information in an ordered binary tree means to search for a given key, and if it is found return the information present at that node.
  • With the orderdness condition, the search algorithm can eliminate half the remaining nodes at each step. The number of operations is proportional to the depth of the tree.
• Lookup:

fun {Lookup X T}
    case T
    of leaf then notfound
    [] tree(Y V T1 T2) andthen X==Y then found(V)
    [] tree(Y V T1 T2) andthen X<Y  then {Lookup X T1}
    [] tree(Y V T1 T2) andthen X>Y  then {Lookup X T2}
    end
end

• To insert or delete information in an ordered binary tree, we construct a new tree that is identical to the original except that it has more or less information.
• Insert:

fun {Insert X V T}
    case T
    of leaf then tree(X V leaf leaf)
    [] tree(Y W T1 T2) andthen X==Y then tree(X V T1 T2)
    [] tree(Y W T1 T2) andthen X<Y  then tree(Y W {Insert X V T1} T2)
    [] tree(Y W T1 T2) andthen X>Y  then tree(Y W T1 {Insert X V T2})
    end
end

• Calling {Insert X V T} returns a new tree that has the pair (X V) inserted in the right place.
  • If T already contains X, then the new tree replaces the old information with V.

Deletion and tree reorganizing

• The delete operation is not as simple as Lookup and Insert, here is a first try (which is wrong):

fun {Delete X T}
    case T
    of leaf then leaf
    [] tree(Y W T1 T2) andthen X==Y then leaf
    [] tree(Y W T1 T2) andthen X<Y  then tree(Y W {Delete X T1} T2)
    [] tree(Y W T1 T2) andthen X>Y  then tree(Y W T1 {Delete X T2})
    end
end

• Calling {Delete X T} should return a new tree that has no node with key X.
  • The error is that when X==Y, the whole subtree is removed instead of just a single node.
• When X==Y, we have to reorganize the subtree so that it no longer has the key Y but is still an ordered binary tree.

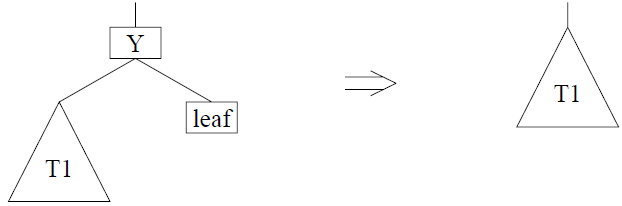
Deleting node Y when one subtree is a leaf (easy case)

Deleting node Y when neither subtree is a leaf (hard case)

• To fix the Delete function, we define a function {RemoveSmallest T2} that returns the smallest key of T2, its associated value, and a new tree that lacks this key:

fun {RemoveSmallest T}
    case T
    of leaf then none
    [] tree(Y V T1 T2) then
        case {RemoveSmallest T1}
        of none then Y#V#T2
        [] Yp#Vp#Tp then Yp#Vp#tree(Y V Tp T2)
        end
    end
end

• The new Delete function that uses the RemoveSmallest function:

fun {Delete X T}
    case T
    of leaf then leaf
    [] tree(Y W T1 T2) andthen X==Y then
        case {RemoveSmallest T2}
        of none then T1
        [] Yp#Vp#Tp then tree(Yp Vp T1 Tp)
        end
    [] tree(Y W T1 T2) andthen X<Y then
        tree(Y W {Delete X T1} T2)
    [] tree(Y W T1 T2) andthen X>Y then
        tree(Y W T1 {Delete X T2})
    end
end

Tree traversal

• Two basic traversals:
  • depth-first: for each node, it visits first the left-most subtree, then the node itself, and then the right-most subtree.
  • breadth-first: it first traverses all nodes at depth 0, then all nodes at depth 1, etc.
• Depth-first traversal that displays each node's key and information:

proc {DFS T}
    case T
    of leaf then skip
    [] tree(Key Val L R) then
        {DFS L}
        {Browse Key#Val}
        {DFS R}
    end
end

• Depth-first traversal that calculates a result (a list of all key/value pairs):

proc {DFSAcc T S1 ?Sn}
    case T
    of leaf then Sn=S1
    [] tree(Key Val L R) then S2 S3 in
        {DFSAcc L S1 S2}
        S3 = Key#Val|S2
        {DFSAcc R S3 Sn}
    end
end

• To implement breadth-first traversal, we need a queue to keep track of all the nodes at a given depth.
  • The next node to visit comes from the head of the queue.
  • The node's two subtrees are added to the tail of the queue.
    • They will be visited when all the other nodes of the queue have been visited (i.e., all the nodes at the current depth).
• Breadth-first traversal implementation with queues from the previous section:

proc {BFS T}
    fun {TreeInsert Q T}
        if T\=leaf then {Insert Q T} else Q end
    end
    
    proc {BFSQueue Q1}
        if {IsEmpty Q1} then skip
        else
            X Q2 = {Delete Q1 X}
            tree(Key Val L R) = X
        in
            {Browse Key#Val}
            {BFSQueue {TreeInsert {TreeInsert Q2 L} R}}
        end
    end
in
    {BFSQueue {TreeInsert {NewQueue} T}}
end

Exercise 3

• Implement breadth-first traversal (BFSAcc) that calculates a list of key/value pairs (with accumulator, similarly as is done with the depth-first algorithm).

Assignment 7

• Write a function (ListToTree) that takes an unordered list of key/value pairs and returnes an ordered binary tree.
  • Tree = {ListToTree [5#o 4#w 1#l 6#l 7#l 0#d 9#h 8#e 3#o 2#r]}
  • You will need the function "Insert" defined in this section to insert each node into the tree that is being constructed.
• Use the function DFSAcc to turn the ordered binary tree into an ordered list.

4. Higher-order programming

• Higher-order programming is the collection of programming techniques that become available when using procedure (or function) values in programs.

Basic operations

• Four basic operations that underlie all the techniques of higher-order programming:
  • Procedural abstraction: the ability to convert any statement into a procedure value.
  • Genericity: the ability to pass procedure values as arguments to a procedure call.
  • Instantiation: the ability to return procedure values as results from a procedure call.
  • Embedding: the ability to put procedure values in data structures.

Procedural abstraction

• Any statement can be packaged into a procedure, which does not execute the statement, but instead creates a procedure value (a closure).
• Executing the procedure value gives exactly the same result as executing the statement.

Genericity

• To make a function generic is to let any specific entity in the function body become an argument of the function.
  • The specific entity is given when the function is called.
• Consider the function SumList, which we will make a generic version of:

fun {SumList L}
    case L
    of nil then 0
    [] X|L1 then X+{SumList L1}
    end
end

• This function has two specific entities: the number zero and the operation plus. The zero is a neutral element for the plus operation.
  • Any neutral element and any operation are possible. We give them as parameters, which gives the following generic function:

fun {FoldR L F U}
    case L
    of nil then U
    [] X|L1 then {F X {FoldR L1 F U}}
    end
end

• SumList definition as a special case of FoldR:

fun {SumList L}
    {FoldR L fun {$ X Y} X+Y end 0}
end

Exercise 4

• Use FoldR to define the function "ProductList" that calculates the product of all elements in the list.
• Use FoldR to define the function "Some" that returnes true if there is at least one true in the list.
  Hint

  {Or true false} returns true.

Instantiation

• An example of instantiation is a function MakeSort that returnes a sorting function:

fun {MakeSort F}
    fun {$ L}
        {Sort L F}
    end
end

Exercise 5

• Use MakeSort to instantiate a sorting function and sort a list of integers (descending).
  Hint

  Function "Sort" accepts a list L and a function F. The function F should accept two sortable values (e.g., two integers) and return a boolean value that dictates how those two values should be sorted.

Embedding

• Procedure values can be put in data structures. This has many uses:
  • Explicit lazy evaluation (delayed evaluation): building a data structure on demand.
  • Modules: records that group together a set of related operations.
  • Software component: a generic procedure that takes a set of modules as input arguments and returnes a new module.

5. Abstract data types

• A data type (or simply type) is a set of values together with a set of operations on these values.
• A type is abstract if it is completely defined by its set of operations, regardless of the implementation.
  • It is possible to change the implementation of the type without changing its use.

A declarative stack

• A stack is a simple example of an abstract data type.
  • <Stack T> contains elements of type T (T being any type).
• Assume the stack has four operations, with following types:
  • < fun {NewStack}: <Stack T> >
  • < fun {Push <Stack T> T}: <Stack T> >
  • < fun {Pop <Stack T> T}: <Stack T> >
  • < fun {IsEmpty <Stack T>}: <Bool> >
• This set of operations and their types defines the interface of the abstract data type. These operations satisfy certain laws:
  • A new stack is always empty.
    • {IsEmpty {NewStack}} = true.
  • Pushing an element and then popping gives the same element back.
    • For any E and S0, S1 = {Push S0 E} and S0 = {Pop S1 E} hold.
  • No elements can be popped off an empty stack.
    • {Pop {EmptyStack}} raises an error.
• All implementations have to satisfy these laws. Here is an implementation of the stack:

fun {NewStack} nil end
fun {Push S E} E|S end
fun {Pop S E} case S of X|S1 then E=X S1 end end
fun {IsEmpty S} S==nil end

• A program that uses the stack will work with any implementation that satisfies the defined laws.
• Notice: "Pop" is written using a functional syntax, but one of its arguments is an output.

Exercise 6

• Write an example program that creates a stack, pushes a few elements, pops a few, and checks if the stack is empty.

A declarative dictionary

• Another (extremely useful) example of an abstract data type is dictionary.
• A dictionary is a finite mapping from a set of simple constants to a set of language entities.
  • Each constant maps to one entity.
  • The constants are called keys, and the entites are called values.
• Assume the dictionary (<Dict>) has four operations, with following types:
  • < fun {NewDict}: <Dict> >
    • Returnes a new empty dictionary.
  • < fun {Put <Dict> <Key> <Value>}: <Dict> >
    • Takes a dictionary and returnes a new dictionary that adds the mapping <Key> -> <Value>. If <Key> already exists, then the new dictionary replaces its mapping with the new one.
  • < fun {Get <Dict> <Key>}: <Value> >
    • Returnes the value corresponding to <Key>. If there is none, an exception is raised.
  • < fun {Domain <Dict>}: <List <Key>> >
    • Returnes a list of keys in <Dict>.

List-based implementation

• Dictionary can be implemented with a list representing the dictionary.
  • List contains Key#Value pairs that are sorted on the key.
• A list-based implementation would be extremely slow for large dictionaries.
  • The number of operations is O(n) for dictionaries with n keys (for both Put and Get).

Tree-based implementation

• A more efficient implementation of dictionaries is possible by using an ordered binary tree.
  • Put is simply Insert, and Get is very similar to Lookup.
• In this implementation, the Put and Get operations take O(log n) time and space for a tree with n nodes.

State-based implementation

• We can do even better than the tree-based implementation by leaving the declarative model behind and using explicit state.
  • Using state can reduce the execution time of Put and Get operations to amortized constant time.

---

< ^ >