3. Explicit State

"If declarative programming is like a crystal, immutable and practically eternal, then stateful programming is organic: it grows and evolves as we watch."
- Inspired by On Growth and Form, D'Arcy Wentworth Thompson (1860-1948)

1. State

Implicit (declarative) state

fun {SumList Xs S}
    case Xs
    of nil then S
    [] X|Xr then {SumList Xr X+S}
    end
end

Explicit state

local
    C = {NewCell 0}
in
    fun {SumList Xs S}
        C := @C+1
        case Xs
        of nil then S
        [] X|Xr then {SumList Xr X+S}
        end
    end
    fun {SumCount} @C end
end

Exercise 1

2. State and system building

System properties

Component-based programming

Object-oriented programming

3. Abstract data types

Variations on a stack

Open declarative unbundled stack

fun {NewStack} nil end
fun {Push S E} E|S end
fun {Pop S ?E}
    case S of X|S1 then E=X S1 end
end
fun {IsEmpty S} S==nil end

declare S1 S2 S3 X
S1 = {NewStack}
{Browse {IsEmpty S1}}
S2 = {Push S1 23}
S3 = {Pop S2 X}
{Browse X}

Secure declarative unbundled stack

local Wrap Unwrap in
    {NewWrapper Wrap Unwrap}
    fun {NewStack} {Wrap nil} end
    fun {Push S E} {Wrap E|{Unwrap S}} end
    fun {Pop S ?E}
        case {Unwrap S} of X|S1 then E=X {Wrap S1} end
    end
    fun {IsEmpty S} {Unwrap S}==nil end
end

proc {NewWrapper ?Wrap ?Unwrap}
    Key = {NewName}
in
    fun {Wrap X}
        fun {$ K} if K==Key then X end end
    end
    fun {Unwrap W}
        {W Key}
    end
end

Secure declarative bundled stack

local
    fun {StackOps S}
        fun {Push X} {StackOps X|S} end
        fun {Pop ?E}
            case S of X|S1 then E=X {StackOps S1} end
        end
        fun {IsEmpty} S==nil end
    in
        ops(push:Push pop:Pop isEmpty:IsEmpty)
    end
in
    fun {NewStack} {StackOps nil} end
end

declare S1 S2 S3 X
S1 = {NewStack}
{Browse {S1.isEmpty}}
S2 = {S1.push 23}
S3 = {S2.pop X}
{Browse X}

Secure stateful bundled stack

fun {NewStack}
    C = {NewCell nil}
    proc {Push X} C:=X|@C end
    fun {Pop}
        case @C of X|S1 then C:=S1 X end
    end
    fun {IsEmpty} @C==nil end
in
    ops(push:Push pop:Pop isEmpty:IsEmpty)
end

S = {NewStack}
{Browse {S.isEmpty}}
{S.push 23}
X = {S.pop}
{Browse X}

Assignment 1

4. Stateful collections

Indexed collections


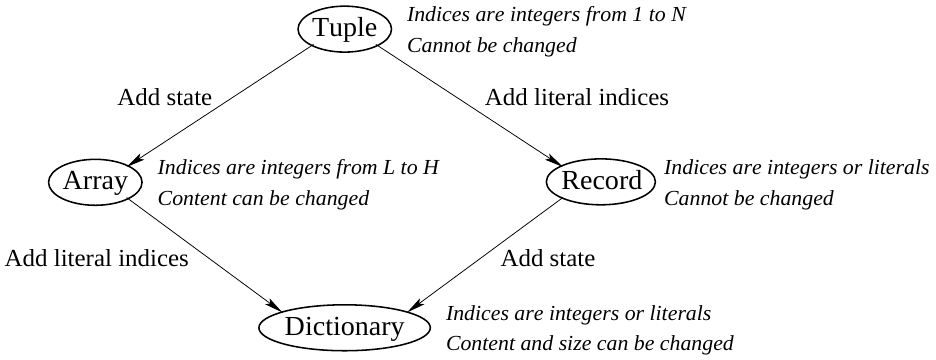
Varieties of indexed collections

Unindexed collections

Extensible collections

5. Case study

Generating random numbers

Different approaches

Uniformly distributed pseudorandom numbers

local
    A = 333667
    B = 213453321
    M = 1000000000
in
    proc {NewRand ?Rand ?Init ?Max}
        X = {NewCell 0}
    in
        proc {Init Seed} X:=Seed end
        fun {Rand} X := (A*@X+B) mod M in @X end
        Max = M
    end
end

declare Rand Init Max
{NewRand Rand Init Max}
{Init 10}
{Browse {Rand}}
{Browse {Rand}}

local
    A = 333667
    B = 213453321
    M = 1000000000
in
    fun lazy {RandList S0}
        S1 = (A*S0+B) mod M
    in
        S1|{RandList S1}
    end
end

declare
L = {RandList 10}
{Browse L.1}
{Browse L.2.1}

Assignment 2

Assignment 3

6. Object-Oriented Programming

< ^ >