Declarative Concurrency

"More thread not always faster."
- By a forum user (2019)

• The declarative model lets us write many programs and use powerful reasoning techniques on them. But some useful programs cannot be written easily or efficiently in it.
  • Some programs are best written as a set of activities that execute independently.
  • Such programs are called concurrent.
  • Concurrency is essential for programs that interact with their environment (e.g., agents, GUI, OS interaction).
  • Concurrency also lets a program be organized into parts that execute independently and interact only when needed (i.e., client/server and producer/consumer programs).
• This chapter extends the declarative model with concurrency while still being declarative.
  • All the programming and reasoning techniques for declarative programming still apply.
  • Declarative concurrency model is still declarative because a dataflow variable can be bound to only one value, which has two consequences:
    • What stays the same: The result of a program is the same whether or not it is concurrent.
    • What is new: The result of a program can be calculated incrementally.

Comparison example

• Example of a sequential program that calculates a list of successive squares by generating a list of successive integers and then mapping each to its square:

declare

fun {Gen L H}
    {Delay 100}
    if L>H then nil else L|{Gen L+1 H} end
end

Xs = {Gen 1 10}
Ys = {Map Xs fun {$ X} X*X end}
{Browse Ys}

• We can make this concurrent by doing the generation and mapping in their own threads:

declare Xs Ys
thread Xs = {Gen 1 10} end
thread Ys = {Map Xs fun {$ X} X*X end} end
{Browse Ys}

• The result of the calculation is the same in both cases.
  • In the sequential version, Gen calculates the whole list before Map starts. The final result is displayed all at once when the calculation is complete, after one second.
  • In the concurrent version, Gen and Map both execute simultaneously. Whenever Gen adds an element to its list, Map will immediately calculate its square. The result is displayed incrementally.
• This form of concurreny is simple because it has no observable nondeterminism. There are no race conditions in a declarative concurrent program.

Nondeterminism

• An execution is nondeterministic if there is an execution state in which there is a choice of what to do next (i.e., which thread to reduce).
  • If there are several threads, then in each execution state the system has to choose which thread to execute next.
• In a declarative concurrent model, the nondeterminism is not visible to the programmer. There are two reasons for this:
  • First, dataflow variables can be bound to only one value.
    • The nondeterminism affects only the exact moment when each binding takes place, it does not affect the fact that the binding does take place.
  • Second, any operation that needs the value of a variable has no choice but to wait until the variable is bound.
    • If we allow operations that could choose whether to wait or not then the nondeterminism would become visible.
• The last assignment (in the previous chapter) is an example of visible nondeterminism (random number generator that uses nondeterminism in concurrency).

Failure

• A failure is an abnormal termination of a declarative program that occurs when we attempt to put conflicting information in the store.
  • For example, if we would bind X both to 1 and to 2.
• If a declarative concurrent program results in failure for a given set of inputs, then all possible executions with those inputs will result in failure.
  • This must be so, else some executions would lead to failure and other would not (with same inputs), which would make the nondeterminism observable.
• Example of conflicting bindings:

thread X=1 end
thread Y=2 end
thread X=Y end

• We see that all executions (order of executing the threads) will eventually reach a conflicting binding and subsequently terminate.
• Often we would like to continue execution instead of terminating, perhaps to repair the error or simply to report it.
  • A natural way to do this is by using exceptions. At the point where a failure would occur, we raise an exception instead of terminating.
  • The program can catch the exception and continue executing.
  • The store contents (variable bindings) are what they were just before the failure.
• Execution after raising the exception is no longer declarative.
  • This is because the store contents are not always the same in all executions.
  • If an exception occurs in mid-execution, the variables can have different values depending on the execution order.
  • If the program continues execution then we can observe these values, which leads to observable nondeterminism.

Failure confinement

• If we want execution to become declarative again after a failure, then we have to hide the nondeterminism.
• Assume that the variables X and Y are visible to the rest of the program.
  • If there is an exception, we arrange for X and Y to be bound to default values.
  • If there is no exception, then they are bound as before.

declare X Y
local X1 Y1 S1 S2 S3 in
    thread
        try X1=1 S1=ok catch _ then S1=error end
    end
    thread
        try Y1=2 S2=ok catch _ then S2=error end
    end
    thread
        try X1=Y1 S3=ok catch _ then S3=error end
    end
    if S1==error orelse S2==error orelse S3==error then
        X=1  % Default for X
        Y=1  % Default for Y
    else X=X1 Y=Y1 end
end

• Info:
  • We catch the failure with the try statements, so that execution will not stop with an error.
    • A try statement is needed for each binding since each binding could fail.
  • We do the bindings in local variables X1 and Y1, which are invisible to the rest of the program.
    • We make the bindings global only when we are sure that there is no failure.

1. Supply-driven concurrency

• Supply-driven concurrency (or data-driven concurrency) is a form of declarative concurrent programming that is focused on the use of dataflow variables.
  • Each thread is a dataflow thread, i.e., it suspends on availability of data.

Simple dataflow behavior

• Consider the following program:

declare X0 X1 X2 X3
thread
Y0 Y1 Y2 Y3 in
    {Browse [Y0 Y1 Y2 Y3]}
    Y0 = X0+1
    Y1 = X1+Y0
    Y2 = X2+Y1
    Y3 = X3+Y2
    {Browse completed}
end

{Browse [X0 X1 X2 X3]}

• Observe what happens when you input the following statements one at a time:

X0 = 0
X1 = 1
X2 = 2
X3 = 3

• With each statement, the thread resumes, executes one addition, and then suspends again.

Using a declarative program in a concurrent setting

• Consider the ForAll loop:

proc {ForAll L P}
    case L of nil then skip
    [] X|L2 then {P X} {ForAll L2 P} end
end

• Execute it in a thread with the unbound variable L:

declare L in
thread {ForAll L Browse} end

• This suspends and waits for L to be bound to a value.
• We can bound L in other threads;

declare L1 L2
thread L=1|L1 end
thread L1=2|3|L2 end
thread L2=4|nil end

• Is the result any different from the result of the sequential call {ForAll [1 2 3 4] Browse}?
  • What is the effect of using ForAll in a concurrent setting?

A concurrent map function

• Here is a concurrent version of the Map function:

fun {Map Xs F}
    case Xs of nil then nil
    [] X|Xr then thread {F X} end|{Map Xr F} end
end

• Info:
  • When thread {F X} end finishes, it returnes the value returned by the function F.
• If we enter the following statements, a new thread executing {Map Xs F} is created:

declare Xs F Ys Zs
{Browse thread {Map Xs F} end}

• It will suspend immediately because Xs is unbound (and so is F).
• If we enter the following statements, the main thread will traverse the list, creating two threads for the first two elements of the list (thread {F 1} end and thread {F 2} end), and then it will suspend again on the tail of the list.

Xs = 1|2|Ys
fun {F X} X*X end

• After we bind the tail (Ys) of the list, a third thread will be created (thread {F 3} end), and the program will terminate with the final list [1 4 9] as the result.

Ys = 3|Zs
Zs = nil

• The result is the same as with the sequential map function, the difference being that the concurrent version can obtain the output incrementally if the input is given incrementally.

Assignment 1

• Implement a declarative concurrent Monte Carlo approximator of the number pi.
  • π ≈ 4 * (number of points in the circle / total number of points)
  • {MCPi NT NP} should return the approximation.
    • NT: The number of threads.
    • NP: The total number of points.
  • For the source of random numbers use the stateful implementation of the pseudorandom number generator from the previous chapter.
  • {Sqrt (X*X + Y*Y)} < 1.0 will be true for the points that are inside of the circle with radius 1.
  • Use only floats.

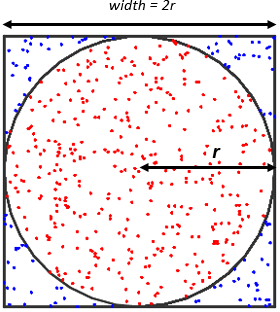
Monte Carlo Pi approximation

2. Streams

• Streams can be used for communication between threads.
• A stream is a potentially unbounded list of messages, i.e., it is a list whose tail is an unbound datafow variable.
  • Sending a message is done by extending the stream by one element.
• Stream programming is a general approach that can be applied in many domains.
  • It is the concept underlying Unix pipes.
• This chapter looks at a special case of stream programming, deterministic stream programming (declarative).

Basic producer/consumer

• In the declarative concurrent model, a stream is represented by a list whose tail is an unbound variable:

declare Xs Xs2 in
Xs = 0|1|2|3|4|Xs2

• A stream is created incrementally by binding the tail to a new list pair:

declare Xs3 in
Xs2 = 5|Xs3

• One thread, called the producer, creates the stream, and other threads, called the consumers, read the stream.
• The following program asynchronously generates a stream of integers and sums them:

fun {Generate N Limit}
    if N<Limit then
        N|{Generate N+1 Limit}
    else nil end
end

fun {Sum Xs A}
    case Xs
    of X|Xr then {Sum Xr A+X}
    [] nil then A
    end
end

local Xs S in
    thread Xs = {Generate 0 150000} end  % Producer thread
    thread S = {Sum Xs 0} end            % Consumer thread
    {Browse S}
end

Multiple readers

• We can introduce multiple consumers without changing the program in any way:

local Xs S1 S2 S3 in
    thread Xs={Generate 0 150000} end
    thread S1={Sum Xs 0} end
    thread S2={Sum Xs 0} end
    thread S3={Sum Xs 0} end
end

• Each consumer will recieve stream elements independently of the others.

Transducers and pipelines

• We can put a third stream object in between the producer and consumer.
  • This stream object (transducer) reads the producer's stream and creates another stream which is read by the consumer.
• A sequence of stream objects each of which feeds the next is called a pipeline.

Filtering a stream

• One of the simplest transducers is the filter, which outputs only those elements of the input stream that satisfy a given condition.
• A simple way to make a filter is to put a call to the function Filter inside its own thread.
• For example, we can pass only those elements that are odd integers:

fun {IsOdd X} X mod 2 \= 0 end

local Xs Ys S in
    thread Xs={Generate 0 150000} end
    thread Ys={Filter Xs IsOdd} end
    thread S={Sum Ys 0} end
    {Browse Ys}
    {Browse S}
end

Sieve of Eratosthenes

• The output of the prime-number sieve of Eratosthenes is a stream containing only prime numbers.
  • It successively filters out nonprimes from streams until only primes remain.
  • The filters are created dynamically when they are needed.
  • The producer generates a stream of consecutive integers starting from 2.
  • The sieve peels off an element and creates a filter to remove multiples of that element.
  • It then calls itself recursively on the stream of remaining elements.

fun {Sieve Xs}
    case Xs
    of nil then nil
    [] X|Xr then Ys in
        thread Ys={Filter Xr fun {$ Y} Y mod X \= 0 end} end
        X|{Sieve Ys}
    end
end

local Xs Ys in
    thread Xs={Generate 2 100000} end
    thread Ys={Sieve Xs} end
    {Browse Ys}
end

3. Demand-driven concurrency

• Demand-driven evaluation, or lazy evaluation, in contrast to the usual execution strategy (eager evaluation or data-driven evaluation), executes a statement when its result is needed somewhere else in the program.
  • Data-driven evaluation executes statements in order.
• For example:

fun lazy {F1 X} 1+X*(3+X*(3+X)) end
fun lazy {F2 X} Y=X*X in Y*Y end
fun lazy {F3 X} (X+1)*(X+1) end
A = {F1 10}
B = {F2 20}
C = {F3 30}
D = A+B

• Info:
  • The three functions F1, F2, and F3 are lazy functions.
  • The lazy functions are not executed when they are called.
    • They create stopped executions that will be continued only when their results are needed.
  • In this example, the function calls A={F1 10}, B={F2 20}, and C={F3 30} all create stopped executions.
    • When the addition D=A+B is invoked, the values of A and B are needed. This triggers the execution of the first two calls. After the calls finish, the addition can continue. Since C is not needed, the third call is not executed.

Lazy streams

• In the producer/consumer example in a previous section, it is the producer that decides how many list elements to generate (i.e., execution is eager).
• Here is how to do that example with a lazy function that generates a potentially infinite list:

fun lazy {Generate N}
    N|{Generate N+1}
end

fun {Sum Xs A Limit}
    if Limit>0 then
        case Xs of X|Xr then
            {Sum Xr A+X Limit-1}
        end
    else A end
end

local Xs S in
    Xs = {Generate 0}      % Producer
    S = {Sum Xs 0 150000}  % Consumer
    {Browse S}
end

• Info:
  • The Generate call does not need to be put in its own thread (in contrast to the eager version).
  • In this example, it is the consumer that decides how many list elements should be generated.
  • With bigger lists, this (lazy) version is faster as it needs only a very small memory space during execution, while the eager version needs a huge memory space.
• The multiple reader example with lazy execution:

local Xs S1 S2 S3 in
    Xs = {Generate 0}
    thread S1 = {Sum Xs 0 150000} end
    thread S2 = {Sum Xs 0 100000} end
    thread S3 = {Sum Xs 0 50000} end
end

Assignment 2

• Implement a pipeline defined below:

declare

Step = 0.1

fun lazy {Generate N} end
fun lazy {ListSin Xs} end
fun lazy {ListCos Xs} end
fun lazy {ListSlope Xs} end
fun lazy {Diff Xs Ys} end
fun {GetList L N} end

local Time Sinus Slope Err L in
   Time = {Generate 0.0}
   Sinus = {ListSin Time}
   Cosinus = {ListCos Time}
   Slope = {ListSlope Sinus}
   Err = {Diff Cosinus Slope}
   
   {Browse Time}
   {Browse Sinus}
   {Browse Cosinus}
   {Browse Slope}
   {Browse Err}

   L = {GetList Err 50}
   {Browse done}
   {Browse L}
end

• {Generate N} lazily generates floats (from 0.0 to infinity, step size can be 0.1).
• {ListSin Xs} lazily calculates sinus values using values from the list Xs as inputs.
  • Use {Sin X}, which returnes the sinus of X, where X is a float.
• {ListCos Xs} lazily calculates cosinus values using values from the list Xs as inputs.
  • Use {Cos X}, which returnes the cosinus of X, where X is a float.
• {ListSlope Xs} lazily calculates slope of the function described by the values from the list Xs. The slope is approximation of derivation. Derivation of sinus is cosinus.
  • Formula for slope using two neighboring points in a function: (f(x+step)-f(x))/step
• {Diff Xs Ys} lazily calculates the difference between all the values in lists Xs and Ys.
  • {Diff [1 2 3] [3 2 1]} = [-2 0 2]
• {GetList L N} returnes a list by taking the first N elements from the list L. Delay each element with a {Delay 100} to slowly construct the list.

Lazy list operations

• We need lazy versions of list operations for the next section (List comprehensions).

Lazy mapping

• Map evaluates a function on all elemets of a list and returnes the new list. Lazy version takes any list or lazy list and returns a lazy list:

fun lazy {LMap Xs F}
    case Xs
    of nil then nil
    [] X|Xr then {F X}|{LMap Xr F}
    end
end

Lazy integer lists

• The function {LFrom I J} generates a lazy list of integers from I to J:

fun {LFrom I J}
    fun lazy {LFromLoop I}
        if I>J then nil else I|{LFromLoop I+1} end
    end
    fun lazy {LFromInf I} I|{LFromInf I+1} end
in
    if J==inf then {LFromInf I} else {LFromLoop I} end
end

Lazy flatten

• The function {LFlatten Xs} takes a list that contains lists and returns a flat list that contains all the elements from all the sublists:

fun {LFlatten Xs}
    fun lazy {LFlattenD Xs E}
        case Xs
        of nil then E
        [] X|Xr then
            {LFlattenD X {LFlattenD Xr E}}
        [] X then X|E
        end
    end
in
    {LFlattenD Xs nil}
end

Lazy filter

• The lazy function {LFilter L F} filters an input list according to a condition F:

fun lazy {LFilter L F}
    case L
    of nil then nil
    [] X|L2 then
        if {F X} then X|{LFilter L2 F} else {LFilter L2 F} end
    end
end

List comprehensions

• List comprehensions are a powerful tool for calculating with lazy streams.
• They allow to specify lazy streams in a way that closely resembles the mathematical notation of set comprehension.
  • The list comprehension [ x*y | 1≤x≤10, 1≤y≤x ] specifies the list [1*1 2*1 2*2 3*1 3*2 3*3 ... 10*10].
• Because of laziness the list comprehension can generate a potentially unbounded stream, not just a finite list.
• List comprehensions have the basic form:
  • [ f(x) | x <- generator(), guard(x) ]
  • The generator calculates a lazy list whose elements are successively assigned to x.
  • The guard is a boolean function.
  • The resulting list will contain elements f(x), where f is any function and x takes values from the generator for which the guard is true.
  • A list comprehension can can have multiple generators and guards. The generators, when taken from left to right, are considered as nested loops.
• The list comprehension: z = [ x#x | x <- from(1,10) ] can be programmed as:

Z = {LMap {LFrom 1 10} fun {$ X} X#X end}

• The list comprehension: z = [ x#y | x <- from(1,10), y <- from(1,x) ] can be programmed as:

Z = {LFlatten
        {LMap {LFrom 1 10} fun {$ X}
            {LMap {LFrom 1 X} fun {$ Y}
                X#Y
            end}
        end}}

• The list comprehension: z = [ x#y | x <- from(1,10), y <- from(1,10), x+y≤10) ] produces the list of all pairs x#y such that the sum x+y is at most 10. It can be programmed as:

Z = {LFilter
        {LFlatten
            {LMap {LFrom 1 10} fun {$ X}
                {LMap {LFrom 1 10} fun {$ Y}
                    X#Y
                end}
            end}}
        fun {$ X#Y} X+Y=<10 end}

4. Other concurrency models

• Declarative concurrency (this chapter) is concurrency in the declarative model, which gives the same results as a sequential program but can give them incrementally. This model is usable when there is no observable nondeterminism.
• Message-passing concurrency: messages are passed between port objects, which are internally sequential.
• Shared-state concurrency: threads update shared passive objects using atomic actions.

Message-passing concurrency

• In the current chapter we saw how to program with stream objects, which is both declarative and concurrent.
  • But it has the limitation that it cannot handle observable nondeterminism. We cannot program a client/server where the server does not know which client will send it the next message.
  • We can remove this limitation by extending the model with an asynchronous communication channel. Then any client can send messages to the channel and the server can read them from the channel.
    • We use a channel called a port that has an associated stream. Sending a message to the port causes the message to appear on the port's stream.
  • The extended model is called message-passing concurrent model. Since this model is nondeterministic, it is no longer declarative.
• A port is an ADT that has two operations, creating a channel and sending to it:
  • {NewPort S P}: create a new port with entry point P and stream S.
  • {Send P X}: append X to the stream corresponding to the entry point P.
• Example port usage:

declare S P
{NewPort S P}
{Browse S}
{Send P a}
{Send P b}

• A port object is a combination of one or more ports and a stream object.
  • This extends stream objects in two ways:
    • Many-to-one communication is possible (many threads can reference a given port object and send to it independently).
    • Port objects can be embedded inside data structures.
• Example port object usage:

declare P
local S in
    {NewPort S P}
    thread for M in S do {Browse M} end end
end

{Send P hi}

• The thread contains a recursive procedure (for loop in this case) that reads the port streams and performs some action for each message received (Browse in this case).

Exercise 1

• Implement two port objects that send to each other "ping" and "pong".
  • Port1 sends "ping" to Port2, and then the Port2 answers with "pong", to which Port1 answers with "ping", etc.

Shared-state concurrency

• The shared-state concurrent model is a simple extension to the declarative concurrent model that adds explicit state in the form of cells (mutable variables).
• This model is equivalent in expressiveness to the message-passing concurrent model, because cells can be efficiently implemented with ports and vice versa.
• In practice the shared-state model is harder to program than the message-passing model.
  • It is easy to imagine why: multiple threads are accessing same mutable variables and the order in which the threads access those variables is unknown.
    • There are many possible executions (ways in which the program's operations are interleaved).
    • We manage the interleavings with atomic actions on shared cells (locking, monitors, transactions).

Distributed programming

• A distributed system is a set of computers that are linked together by a network.
• Ideally, distributed programming would be just a kind of concurrent programming, and the techniques we have seen would still apply.
  • Nope, distributed programming has its own problems:
    • Each process has its own adress space.
    • The network has limited performance.
    • Some resources are localized (such as the file system).
    • The distributed system can fail partially.
    • The distributed system is open (independent users and computers cohabit the system).

---

< ^ >